目的
音声を処理するには,まず人間が音声を生成する過程を知る必要がある.ここでは,音声の生成過程を学び,声の高さに相当する基本周波数を推定する.
説明
音声の生成過程
発声器官
人間が声を発するときに使用する発声器官は,以下のサイトの図に示すように,肺・気管・声帯・喉頭・咽頭・鼻腔・口腔などからなるひとつながりの管である.
http://gc.sfc.keio.ac.jp/class/2002_14630/slides/10/35.html
喉頭にある声帯は筋肉と粘膜でできた左右一対のヒダのようなものであり,声門は声帯の隙間を指す.
音声の生成過程(音源の生成)
音声の生成過程を考えよう.まず腹筋が横隔膜を押し上げると,肺から空気が押し出される.この空気が気管を通り,喉頭の声帯(声門)に至る.通常呼吸をしているとき,筋肉が緩んだ状態で左右の声帯の間隔は大きく開いているが,声を出すとき,筋肉が縮んで左右の声帯の間隔が接近する.この隙間を空気が通り抜けることにより,ほぼ規則的な空気の振動が生じる.これを声帯音源あるいは音源信号と呼ぶ.音源信号は直接聞くことはできないが,濁ったブザー音のような音であると考えられる.
声の大きさと声の高さ
声帯が大きく振動している場合に声は大きくなり,声帯が速く振動している場合に声は高くなる.ここでは,声の高さについて考えてみよう.声帯の緊張が大きく,肺からの空気圧が高いとき,声帯の開閉周期が短くなり,音源の音の高さが高くなる.このとき,声帯の開閉周期(単位は秒)を基本周期と呼び,基本周波数の逆数を基本周波数と呼ぶ.これらの量が声の高さに関係する.
音声の生成過程(調音)
声道とは喉頭より上の部分を指し,顎・舌・口唇などを動かすことにより,声道は様々な形に変化する.声道は管楽器と同様に音の共鳴器の役割を果たしており,声道の形により音源信号が共鳴し,様々な音色が付与された音声が最終的に出力される.
音韻の特徴
音韻を識別するには,声道の形を推定する必要がある.言い換えれば,声道の形によって変わる共鳴(共振)の仕方を推定する必要がある.共振周波数を推定することができれば,例えば日本語の5母音の識別が可能となる.
まとめ
以上のように,例えば声の大きさや声の高さを推定するには,音声から音源の特徴だけを抽出する必要があり,例えば日本語5母音を識別するには,音声から声道の形(共振周波数)を推定する必要がある.音源の特徴と声道の特徴を分離することが,音声処理の基本となる.
有声音の周期性と調波構造(倍音構造)
ここでは,音源の特徴の1つであり,声の高さに関係する基本周波数や基本周期を推定することを考える.まず,基本周波数や基本周期を求めるために理解する必要がある有声音の性質を考えよう.
有声音の周期性
声帯が振動している音を有声音と呼び,日本語5母音は有声音である.ここでは,有声音の性質を確認しよう.日本語の母音「あ」の音声波形は以下のようになる.
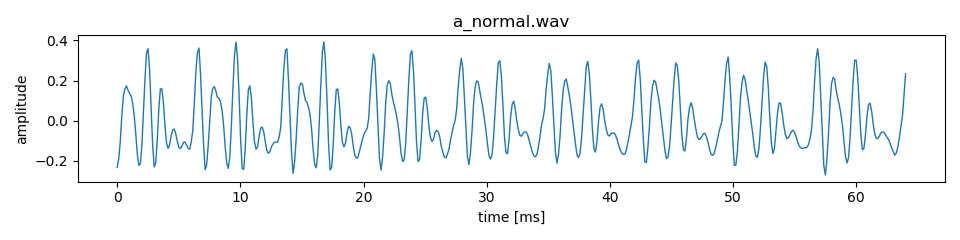
この音声波形から母音「あ」では同じような形の波形が繰り返されていることがわかる.この周期があるという性質は母音「あ」だけではなく,有声音全般に存在する性質である.
周期性と調波構造(倍音構造)
次に,周期のある波について考えてみよう.
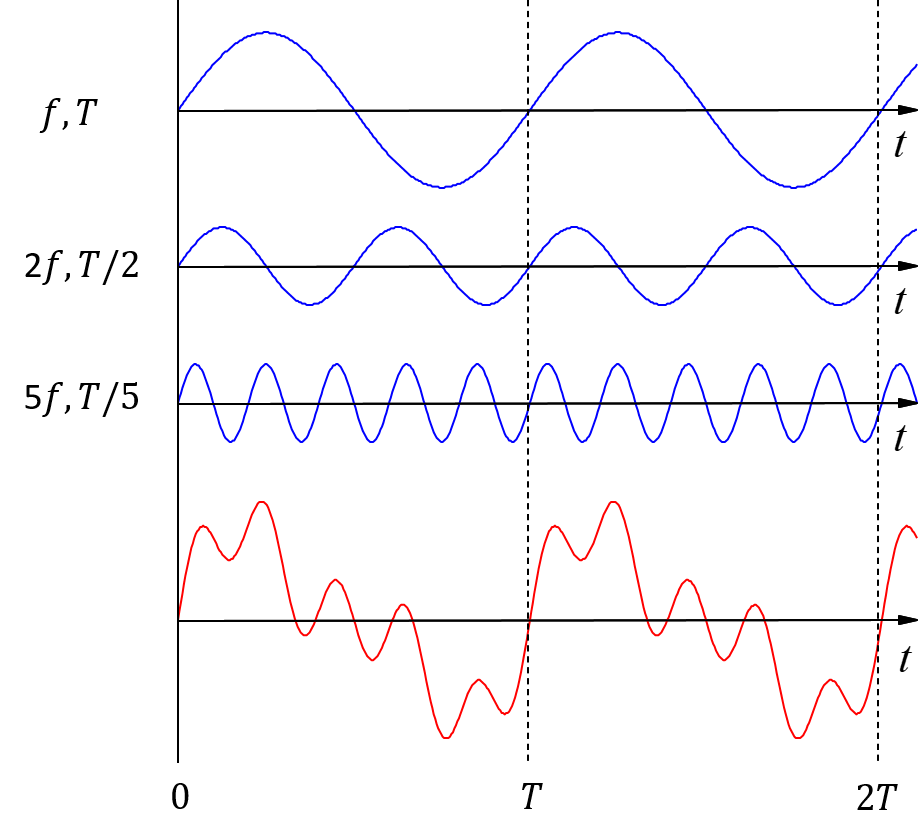
図の3つの青い正弦波を重ね合わせたできる信号が赤い波である.図から赤い波には周期があることが確認できる.赤い波の周期を基本周期\(T\)と呼び,基本周期の逆数を基本周波数\(f\)と呼ぶ.1番上の青い正弦波は基本周期\(T\)で繰り返していることから,この正弦波の周期は基本周期\(T\)であり,周波数は基本周波数\(f\)である.2つ目の青い正弦波は,図より1つ目の正弦波の2倍の速さで振動していることから,周波数は基本周波数の2倍(\(2f\))であり,周期は基本周期の2分の1(\(\frac{T}{2}\))である.3つ目の青い正弦波は,図より1つ目の正弦波の5倍の速さで振動していることから,周波数は基本周波数の5倍(\(5f\))であり,周期は基本周期の5分の1(\(\frac{T}{5}\))である.まとめると,青い正弦波の周波数は基本周波数の整数倍であり,周期は基本周期の整数分の1であることがわかる.
今,赤い波には周期があるが,青い正弦波の周波数が基本周期の整数倍でないとき(あるいは周期が基本周期の整数分の1でないとき)を考えてみよう.上の図で,青い正弦波の周期が基本周波数の整数分の1から少しでもずれると,赤い波の周期性が崩れることがわかる.このことから,赤い波に周期性がある場合,それを構成する単純な波(正弦波)には基本周波数の整数倍の周波数をもつという性質があることがわかる.この性質を調波構造あるいは倍音構造があると言う.
有声音の調波構造(倍音構造)
日本語の母音「あ」には周期性があった.ここでは「あ」に調波構造(倍音構造)があることを確認しよう.
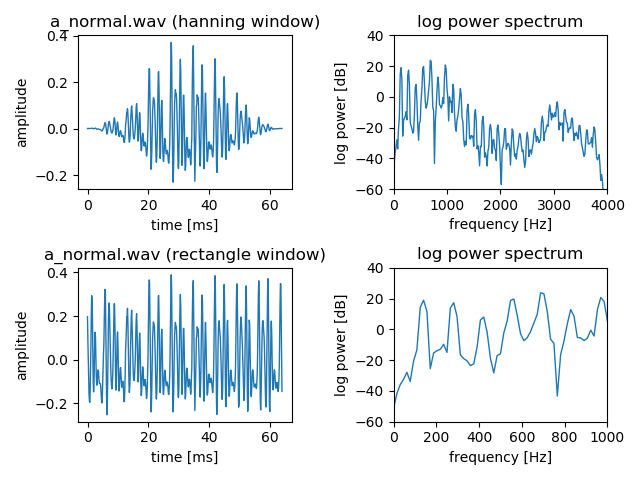
左上が母音「あ」にHanning Windowをかけた波形,右上がその対数パワースペクトルである.基本周期を確認するために,母音「あ」に窓関数をかけない波形を左下に,基本周波数を確認するために対数パワースペクトルの一部(0Hzから1000Hzまで)を表示したものを右下に示した.左下の波形を見ると約63秒間に9回同じような形の波形が現れている.このことから,この音声の基本周期は約7秒であることがわかる.基本周波数はその逆数であるから,約140Hzであると考えられる.一方,右下の対数パワースペクトルを見ると,基本周波数の整数倍である約140Hz, 280Hz, 420Hz, 560Hz, 700Hz, 840Hzにピークがあることがわかる.このことから母音「あ」には周期性があり,調波構造(倍音構造)があることがわかる.この性質は有声音全般に共通する性質である.
基本周波数の推定
声の高さに対応する基本周波数を推定するには,音声波形から基本周期を推定し,その逆数を求めるか,対数パワースペクトルから調波構造を表すピークを求めればよい.ここでは,基本周波数を求める代表的な方法として,自己相関関数を用いた方法とケプストラムを用いた方法を考えよう.
自己相関関数を用いた基本周波数の推定
音声データ\(x(n), n=0,1,\cdots,N-1\)に対して,時間方向に\(\tau\)だけずらした音声データをかけ,時間方向に平均したものを自己相関関数\(R(\tau)\)と呼ぶ.
$$R(\tau)=\frac{1}{N} \sum_{n=0}^{N-1-\tau} x(n)x(n+\tau), \tau=0,1,\cdots,N-1$$
\(x(n)\)に周期がある場合,\(\tau\)が周期に近いと同じような波形がかけ算されるため大きな値となり,周期から遠いと異なる波形がかけ算されるため小さな値となる.
自己相関関数は以上のような方法で求める他に,音声データ\(x(n)\)を離散フーリエ変換し,得られた周波数信号\(X(k)\)のパワー\(|X(k)|^2\)を離散フーリエ逆変換することによっても求めることができる.ここでは後者の方法で自己相関関数を求めてみよう.
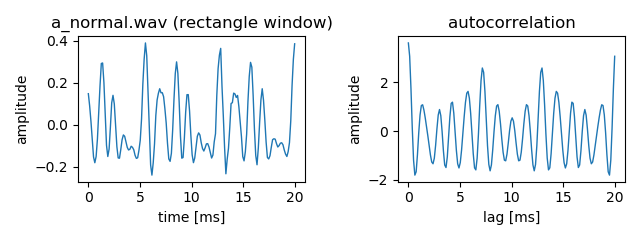
36行目で取り出す時間を20msとし,37行目で20msの標本点数を求め,38行目でグラフの横軸のデータを作成している.39行目から40行目で発話区間の中央20msのデータを方形窓で取り出している.42行目で離散フーリエ変換をかけ,43行目でパワーを求め,離散フーリエ逆変換を行うことで自己相関関数を求めている.62行目から66行目で自己相関関数を描画している.
実行結果は以下のようになり,7ms付近に自己相関関数のピークがあることがわかる.人間の声の高さに対応する基本周期の範囲は2msから12ms程度であるため,その範囲において自己相関関数が最大となる\(\tau\)を求めれば,基本周期が得られる.45行目と46行目で基本周期の範囲を指定し,47行目と48行目で標本点の範囲を求めている.49行目でその範囲において自己相関関数が最大となる位置(インデックス番号)を求め,50行目で時間に変換することで基本周期を求めている.51行目で基本周波数を求め,52行目と53行目で基本周期と基本周波数を表示している.
実行結果は以下のようになり,目視で確認した基本周期と基本周波数とほぼ同じ値が得られていることがわかる.
ケプストラムを用いた基本周波数の推定
声帯の音源信号を\(s(n)\),声道のインパルス応答を\(v(n)\)とすると,音声信号\(x(n)\)はこれらの畳込みによって表される. $$x(n)=\sum_{m=-\infty}^{\infty}s(m)v(n-m)$$畳込みは周波数領域では積として表されるため,\(x(n),s(n),v(n)\)をそれぞれ離散フーリエ変換し,周波数領域で表した信号を\(X(k),S(k),V(k)\)とすると
$$X(k)=S(k)V(k)$$
となる.\(X(k)\)のパワースペクトルは
$$|X(k)|^2=|S(k)|^2 |V(k)|^2$$
となり,対数パワースペクトルは
$$\log|X(k)|^2=\log|S(k)|^2 + \log|V(k)|^2$$
となる.対数パワースペクトルでは,音源信号と声道特性が和の形で表されることがわかる.音源信号は対数パワースペクトルの調波構造として表現されるため,高周波成分に現れる.声道特性は周波数スペクトルの大局的な形(スペクトル包絡)として表されるため,低周波成分として現れる.このことから,対数パワースペクトルを1つの信号と考えると,これを離散フーリエ変換することにより,高周波成分に音源信号が,低周波成分に声道特性が現れることになる.
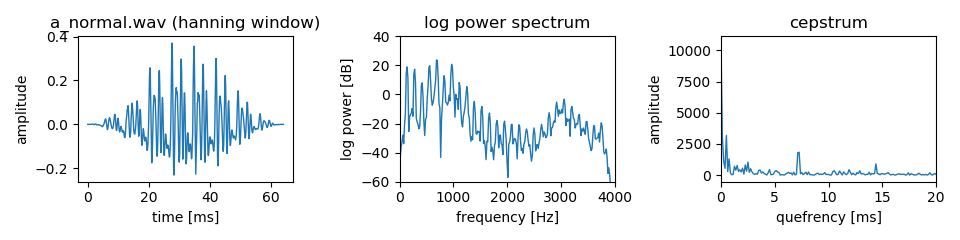
対数パワースペクトルを離散フーリエ変換したものをスペクトル(spectrum)をもじってケプストラム(cepstrum)と呼ぶ.また,ケプストラムのグラフの横軸は時間を表すが,スペクトルの横軸が周波数(frequecny)となることをもじってケフレンシー(quefrency)と呼ぶ.
日本語母音「あ」のケプストラムを求めてみよう.
36行目から40行目で,発話区間の中央の512標本点の音声を取り出し,Hanning Windowをかけている.42行目から44行目で対数パワースペクトルを求めている.46行目で対数パワースペクトルを離散フーリエ変換することでケプストラムを求め,47行目でケプストラムの振幅を求めている.74行目から79行目でケプストラムの振幅を描画している.
実行結果は以下のようになり,ケプストラムの7ms付近や14ms付近にピークが表れていることがわかる.これは,対数パワースペクトルの調波構造のケフレンシーを表しているため,元の音声の基本周期に対応している.人間の声の高さに対応する基本周期の範囲は2msから12ms程度であるため,その範囲でケプストラムが最大となるケフレンシーを求めれば,基本周期が得られる.49行目から57行目で基本周期と基本周波数を求め,表示している.
実行結果は以下のようになり,目視で確認した基本周期と基本周波数とほぼ同じ値が得られていることがわかる.
参考文献
- 板橋秀一,“音声工学”,森北出版,2005年2月
- 古井貞煕,“新音響・音声工学”,近代科学社,2006年9月
課題
以下の音声データを使用して課題を行え.
- 「あ」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/a_normal.wav
- 「い」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/i_normal.wav
- 「う」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/u_normal.wav
- 「え」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/e_normal.wav
- 「お」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/o_normal.wav
- 高い声で「あ」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/a_high.wav
- 低い声で「あ」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/a_low.wav
- 高い声で「い」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/i_high.wav
- 低い声で「い」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/i_low.wav
- 高い声で「う」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/u_high.wav
- 低い声で「う」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/u_low.wav
- 高い声で「え」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/e_high.wav
- 低い声で「え」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/e_low.wav
- 高い声で「お」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/o_high.wav
- 低い声で「お」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/o_low.wav
課題0
高い声と普通の声と低い声で「あ」と発声している音声データの波形と対数パワースペクトルを表示し,目視で基本周期と基本周波数を求めよ.
課題1
高い声と普通の声と低い声で「い」と発声している音声データの波形と対数パワースペクトルを表示し,目視で基本周期と基本周波数を求めよ.
課題2
高い声と普通の声と低い声で「う」と発声している音声データの波形と対数パワースペクトルを表示し,目視で基本周期と基本周波数を求めよ.
課題3
高い声と普通の声と低い声で「え」と発声している音声データの波形と対数パワースペクトルを表示し,目視で基本周期と基本周波数を求めよ.
課題4
高い声と普通の声と低い声で「お」と発声している音声データの波形と対数パワースペクトルを表示し,目視で基本周期と基本周波数を求めよ.
課題5
高い声と普通の声と低い声で「あ」と発声している音声の基本周波数を自己相関関数を用いて求め,課題0の結果と比較せよ.
課題6
高い声と普通の声と低い声で「い」と発声している音声の基本周波数を自己相関関数を用いて求め,課題1の結果と比較せよ.
課題7
高い声と普通の声と低い声で「う」と発声している音声の基本周波数を自己相関関数を用いて求め,課題2の結果と比較せよ.
課題8
高い声と普通の声と低い声で「え」と発声している音声の基本周波数を自己相関関数を用いて求め,課題3の結果と比較せよ.
課題9
高い声と普通の声と低い声で「お」と発声している音声の基本周波数を自己相関関数を用いて求め,課題4の結果と比較せよ.
課題10
高い声と普通の声と低い声で「あ」と発声している音声の基本周波数をケプストラムを用いて求め,課題0,5の結果と比較せよ.
課題11
高い声と普通の声と低い声で「い」と発声している音声の基本周波数をケプストラムを用いて求め,課題1,6の結果と比較せよ.
課題12
高い声と普通の声と低い声で「う」と発声している音声の基本周波数をケプストラムを用いて求め,課題2,7の結果と比較せよ.
課題13
高い声と普通の声と低い声で「え」と発声している音声の基本周波数をケプストラムを用いて求め,課題3,8の結果と比較せよ.
課題14
高い声と普通の声と低い声で「お」と発声している音声の基本周波数をケプストラムを用いて求め,課題4,9の結果と比較せよ.