目的
ここまでで,空間領域で表現された画像データにフィルタ処理を施す空間フィルタ処理について学んだ.ここでは,画像データを離散フーリエ変換により周波数領域に変換し,周波数領域で行う周波数フィルタ処理を学ぶ.
説明
1次元離散フーリエ変換
オーディオデータのような時間信号\(x_n (n=0, 1, \cdots, N-1)\)から周波数信号\(X_k (k=0, 1, \cdots, N-1)\)を求める離散フーリエ変換は
$$X_k = \sum_{n=0}^{N-1} x_n e^{-i \frac{2 \pi kn}{N}}$$
と表せる.また,周波数信号\(X_k\)から時間信号\(x_n\)を求める離散フーリエ逆変換は
$$x_n = \frac{1}{N} \sum_{k=0}^{N-1} X_k e^{i \frac{2 \pi kn}{N}}$$
と表せる.
振幅と位相
周波数信号\(X_k\)は複素数であり,図のように複素平面における原点から\(X_k\)までの距離\(|X_k|\)が振幅,偏角\(\angle X_k\)が位相を表す.

\(X_k\)の実数成分を\(X_{k,r}\),虚数成分を\(X_{k,i}\)とすると,振幅は
$$|X_k| = \sqrt{X_{k,r}^2 + X_{k,i}^2}$$
として求められ,
位相は
$$\angle X_k = \tan^{-1} \frac{X_{k,i}}{X_{k,r}}$$
と求められる.
また,振幅を2乗したものをパワーと呼ぶ.
$$X_k^2 = X_{k,r}^2 + X_{k,i}^2$$
振幅スペクトルと位相スペクトル
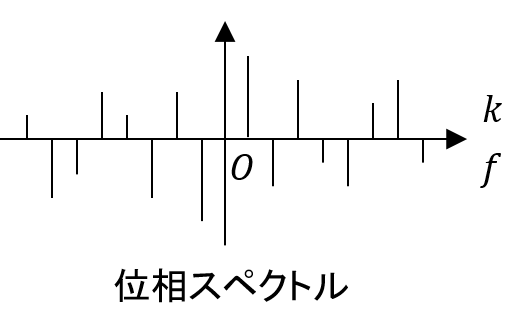
横軸を周波数,縦軸を振幅として描画したグラフを振幅スペクトルと呼ぶ.また,横軸を周波数,縦軸を位相として描画したグラフを位相スペクトルと呼ぶ.周波数信号\(X_k\)と\(X_{-k}\)は複素平面上で実数軸に関して対称であるという性質がある.これを共役な複素数と呼ぶ.図より,共役な複素数の振幅は同じであり,位相は符号が逆となる.

したがって,振幅スペクトルは\(f=0\)あるいは\(k=0\)に関して線対称となり,
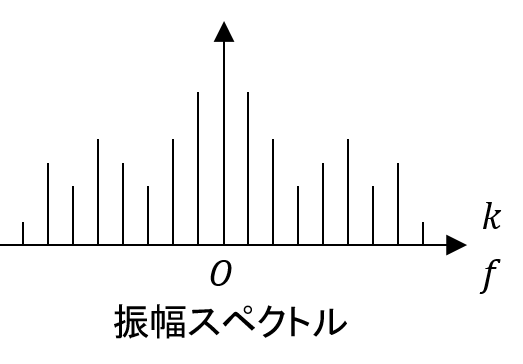
位相スペクトルは原点に関して点対称となる.
2次元離散フーリエ変換
ディジタル画像のような2次元空間信号\(x_{m,n} (m=0, \cdots, M-1, n=0, \cdots, N-1)\)から2次元周波数信号\(X_{k,l} (k=0, \cdots, M-1, l=0, \cdots, N-1)\)を求める2次元離散フーリエ変換は
$$X_{k,l} = \sum_{n=0}^{N-1} \sum_{m=0}^{M-1} x_{m,n} e^{-i \frac{2 \pi km}{M}} e^{-i \frac{2 \pi ln}{N}}$$
と表せる.また,2次元周波数信号\(X_{k,l}\)から2次元空間信号\(x_{m,n}\)を求める2次元離散フーリエ逆変換は
$$x_{m,n} = \frac{1}{MN} \sum_{l=0}^{N-1} \sum_{k=0}^{M-1} X_{k,l} e^{i \frac{2 \pi km}{M}} e^{i \frac{2 \pi ln}{N}}$$
と表せる.
周波数信号\(X_{k,l}\)から振幅・位相を求める方法は1次元の場合と同じであり,振幅スペクトルや位相スペクトルの性質も1次元の場合と同じである.
以下に示すカラー画像を読み込み,グレースケール画像に変換したものに2次元離散フーリエ変換をかけ,振幅スペクトルを描画してみよう.
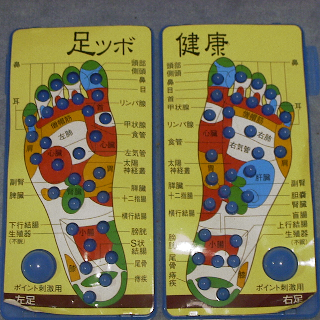
35行目でカラー画像を読み込み,36行目でグレースケール画像に変換し,38行目で2次元離散フーリエ変換をかけている.処理結果は高周波成分が中央となっているが,振幅スペクトルを描画する際には低周波成分が中央に来るようにすることが多い.39行目で低周波成分が中央に来るようにデータをシフトさせ,40行目で振幅を求めている.8行目から14行目に線形濃度変換を行う関数を定義し,17行目から20行目に値が0から255の間の値となるように線形濃度変換を行い,8bitグレースケール画像に変換する関数を定義している.41行目でその関数を呼び出すことで振幅スペクトルの画像を求め,48行目で描画している.実行すると以下のように表示される.現実のシーンをディジタルカメラで撮影した画像の振幅では直流成分の値が大きいため,振幅スペクトルは中央だけが白,その他は黒の画像となることが多い.

そのため,振幅スペクトルを画像として表示するときには対数スケールで描画することが多い.43,44行目で振幅を対数スケールに変換し,45行目で線形濃度変換し,49行目で表示している.実行すると以下のように表示され,振幅スペクトルが求められていることがわかる.

次に,2次元離散フーリエ変換して得られた周波数信号を逆変換し,元の画像が復元できるか確認してみよう.
45行目で周波数信号を2次元離散フーリエ逆変換し,46行目で実数成分を取り出し,データ型を変換し,50行目で表示している.実行すると以下のように表示され,元の画像データが復元されていることがわかる.
振幅スペクトル
画像データよる振幅スペクトルの違いを見てみよう.以下は方向を変えてブライドを撮影した画像の振幅スペクトルである.
左の画像では,横方向にはほとんど輝度の変化はないが,縦方向の輝度の変化は大きい.したがって横方向に低周波で縦方向に高周波の領域の振幅が大きいことがわかる.また,真ん中の画像では,縦方向にはほとんど輝度の変化はないが,横方向の輝度の変化は大きい.したがって縦方向に低周波で横方向に高周波の領域の振幅が大きくなる.右の画像では,左上から右下に向かう方向に対する輝度の変化は小さいが,右上から左下に向かう方向に対する輝度の変化は大きい.したがって左上から右下の方向に低周波で右上から左下の方向に高周波の領域の振幅が大きくなる.
簡単な周波数フィルタ処理
では,画像データに離散フーリエ変換をかけ,周波数領域で表現された画像にフィルタ処理を施してみよう.最も簡単な低域通過フィルタとして,円形に低周波成分のみを通過させるフィルタをかけるには,ある半径の円の外側を0とすることで高周波成分を削除し,離散フーリエ逆変換をかければよい.
57行目で離散フーリエ変換をかけ,58行目で中央が低周波成分となるようにデータをシフトしている.60行目から64行目で指定した半径の円の外側がTrue,内側がFalseとなるマスクを作成している.66行目で周波数領域で表現された画像データをコピーし,67行目で指定した半径の円の外側の値を0にしている.68行目で中央が高周波成分となるようにデータをシフトし,69行目で離散フーリエ逆変換を行い,70行目で実数成分を取り出している.24行目から28行目で,255より大きな値は255に,0より小さい値は0にし,型変換をすることで8bitグレースケール画像に変換する関数を定義し,71行目でその関数を呼び出すことで8bitグレースケール画像に変換している.8行目から12行目に振幅スペクトルと対数振幅スペクトルを求める関数を定義し,73,74行目でその関数を呼び出し,入力画像と出力画像の対数振幅スペクトルを求めている.31行目から38行目に2種類のデータを0から255の間の値となるように線形濃度変換し,8bitグレースケール画像に変換する関数を定義し,75行目でその関数を呼び出すことで,入力画像と出力画像の対数振幅スペクトルを8bitグレースケール画像に変換している.実行すると以下のように表示され,指定した半径の円の内側だけを通過させる低域通過フィルタ処理がなされていることがわかる.
指定した半径の外側だけを通過させる高域通過フィルタを画像にかけるには以下のようにすればよい.
63行目で指定した半径の円の内側がTrue,外側がFalseとなるマスクを作成し,66行目で指定した半径の内側の値を0にしている.68行目で離散フーリエ逆変換を行い,69行目で振幅を求め,70行目で0から255の値となるように線形濃度変換することで8bitグレースケール画像を求めている.実行すると以下のように表示され,指定した半径の円の外側だけを通過させる高域通過フィルタ処理がなされていることがわかる.
周波数フィルタ処理
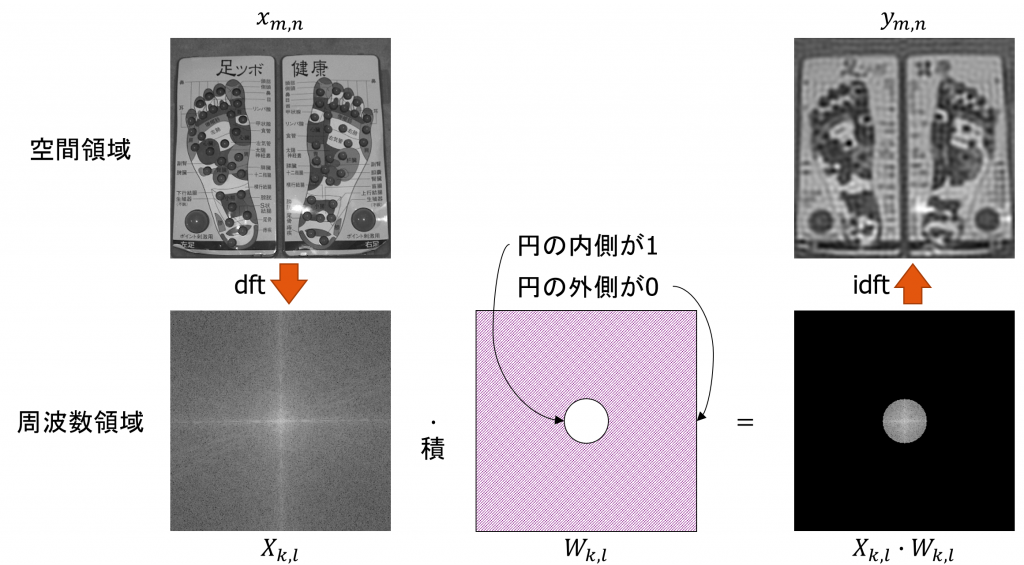
円形に低周波成分のみを通過させる低域通過フィルタを定式化してみよう.空間領域で表現された元の画像を\(x_{m,n}\)とし,\(x_{m,n}\)に離散フーリエ変換をかけ,周波数領域に移したものを\(X_{k,l}\)とする.今,ある半径の円の内側が1・外側が0である周波数フィルタ\(W_{k,l}\)を用意し,\(X_{k,l}\)と\(W_{k,l}\)の積を求める.1をかけるとデータはそのまま通過し,0をかけるとデータは遮断されることから,円の内側のデータだけが通過する低域通過フィルタ処理がなされることがわかる.最後に\(X_{k,l} \cdot W_{k,l}\)に離散フーリエ逆変換をかけると空間領域で表現された処理後の画像\(y_{m,n}\)を得ることができる.空間領域を上に,周波数領域を下にまとめると,周波数フィルタ処理は以下のように図示することができる.
円形に低周波成分のみを通過させる簡単な低域通過フィルタでは,\(W_{k,l}\)は0と1で構成されており,画像の周波数成分を完全に遮断あるいはそのまま通していた.周波数成分を完全に遮断しない場合やそのまま通さない場合には,\(W_{k,l}\)の値は0と1である必要はない.例えば低域を強調したい場合には低域になるほど値が大きくなるように,高域を強調したい場合には高域になるほど値が大きくなるように\(W_{k,l}\)を設計すればよい.\(W_{k,l}\)の値を変えることにより,様々なフィルタを構成することができる.また,空間フィルタ処理で学んだ畳込み演算によるフィルタ処理も周波数領域で行うことができる.
3×3の平均値フィルタ
3×3の平均値フィルタを周波数領域でかけてみよう.
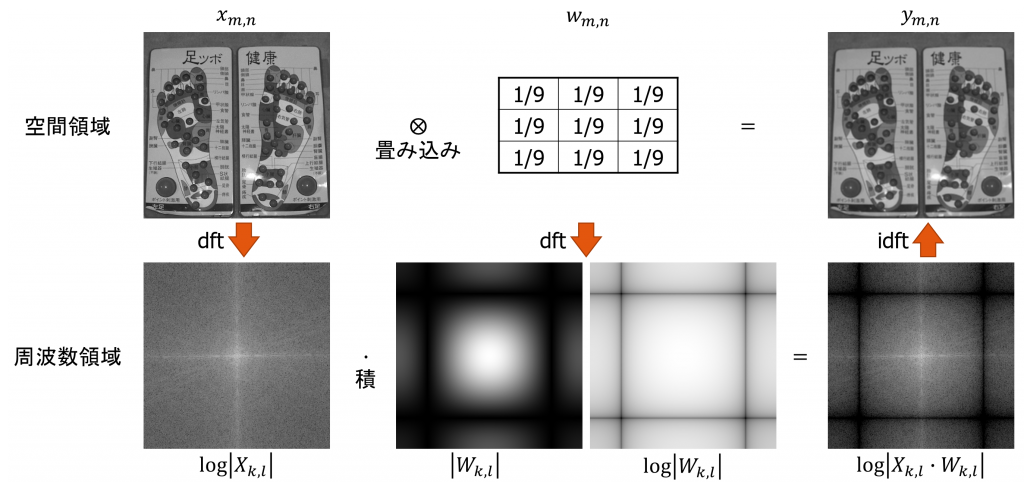
空間領域における畳込み演算は周波数領域における積の演算となるため,3×3の平均値フィルタを周波数領域でかけるには,画像データと3×3の平均値フィルタのカーネルを離散フーリエ変換し,周波数領域で両者の積を求め,離散フーリエ逆変換すればよい.
62行目で画像に離散フーリエ変換をかけ,周波数信号に変換している.64行目で処理対象の画像と同じ大きさで値が0の配列を作り,65から67行目で左上の3×3の領域に3×3の平均値フィルタのカーネルの値を代入している.68行目でカーネルに離散フーリエ変換をかけ,フィルタの周波数特性を求めている.70行目で周波数領域で表現された画像データとフィルタの周波数特性の積を求め,71から73行目で離散フーリエ逆変換を行い,処理後の画像を求めている.また,75行目から81行目で,処理前の画像・カーネル・処理後の画像の振幅スペクトルを求めている.
実行すると以下のような画像が表示され,3×3の平均値フィルタの処理がなされていることがわかる.また,フィルタの振幅特性から,低域を強調するフィルタがかけられていることもわかる.
3×3のSobelフィルタ
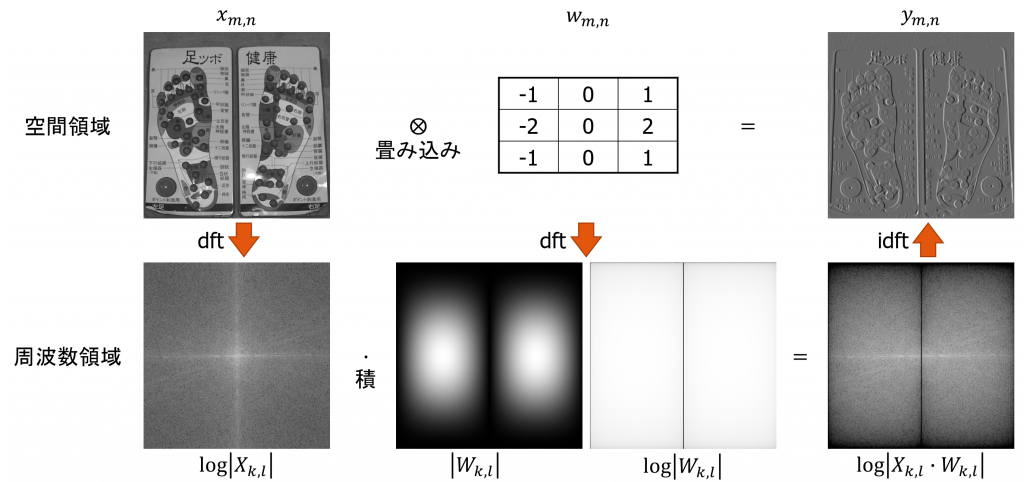
3×3のSobelフィルタを周波数領域でかけるには以下のようにすればよい.
57行目で画像に離散フーリエ変換をかけ,周波数信号に変換している.59行目から63行目で,3×3のSobelフィルタの\(x\)方向の勾配を求めるカーネルに離散フーリエ変換をかけ,フィルタの周波数特性を求めている.64行目から67行目で画像にフィルタをかけることで\(x\)方向の勾配を求めている.実行すると以下のように表示され,\(x\)方向の勾配が求められていることがわかる.
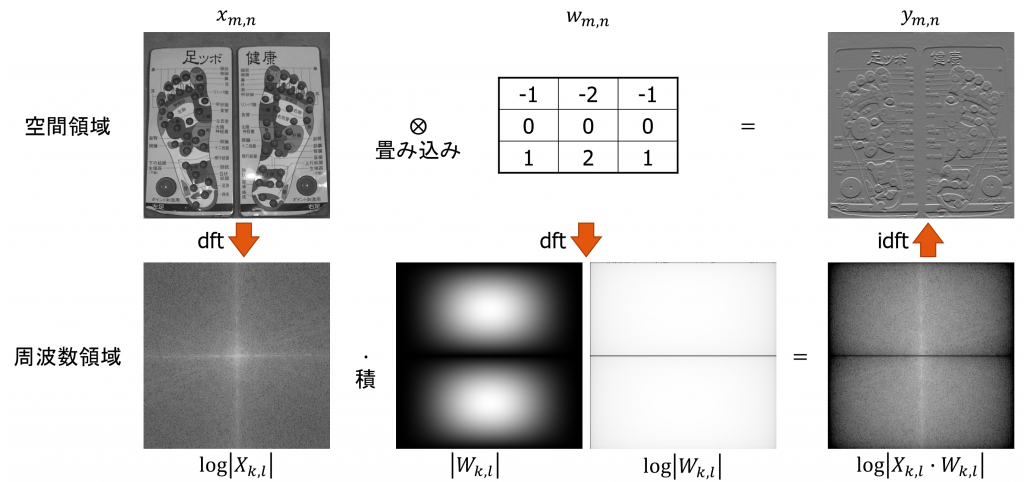
69行目から73行目で,3×3のSobelフィルタの\(y\)方向の勾配を求めるカーネルに離散フーリエ変換をかけ,フィルタの周波数特性を求めている.74行目から77行目で画像にフィルタをかけることで\(y\)方向の勾配を求めている.実行すると以下のように表示され,\(y\)方向の勾配が求められていることがわかる.
79,80行目で勾配ベクトルから勾配の大きさを求めている.実行すると以下のように表示され,勾配の大きさが求められていることがわかる.
鮮鋭化フィルタ
鮮鋭化フィルタを周波数領域でかけるには以下のようにすればよい.
62行目で画像に離散フーリエ変換をかけ,周波数信号に変換している.64行目から68行目で,鮮鋭化フィルタのカーネルに離散フーリエ変換をかけ,フィルタの周波数特性を求めている.70行目から73行目で画像にフィルタをかけることで鮮鋭化を行っている.実行すると以下のように表示され,鮮鋭化処理が行われていることがわかる.
課題
課題0
画像を読み込み,周波数領域で平均値フィルタをかけ,平滑化せよ.
課題1
画像を読み込み,周波数領域で中央の重みが2倍の3×3の平均値フィルタをかけ,平滑化せよ.
課題2
画像を読み込み,周波数領域でガウシアンフィルタをかけ,平滑化せよ.
課題3
画像を読み込み,周波数領域で以下の式で表される1次微分フィルタをかけ,エッジ検出せよ.
$$\frac{\partial f}{\partial x}=f[x+1,y]-f[x,y]$$
$$\frac{\partial f}{\partial y}=f[x,y+1]-f[x,y]$$
課題4
画像を読み込み,周波数領域で以下の式で表される1次微分フィルタをかけ,エッジ検出せよ.
$$\frac{\partial f}{\partial x}=f[x+1,y]-f[x-1,y]$$
$$\frac{\partial f}{\partial x}=f[x,y+1]-f[x,y-1]$$
課題5
画像を読み込み,周波数領域でRobertsフィルタをかけ,エッジ検出せよ.
課題6
画像を読み込み,周波数領域でPrewittフィルタをかけ,エッジ検出せよ.
課題7
画像を読み込み,周波数領域でSobelフィルタをかけ,エッジ検出せよ.
課題8
画像を読み込み,周波数領域でラプラシアンフィルタをかけよ.
課題9
画像を読み込み,周波数領域で鮮鋭化せよ.