目的
ここまでで,音声は音源信号と声道特性から成っていることを学び,音源信号の特徴として声の高さに対応する基本周波数の推定を行った.ここでは,声道の特徴であるスペクトル包絡の推定を行う.
説明
声道特性とスペクトル包絡
ここまでで,音声は音源信号と声道のインパルス応答の畳込みとして表現され,対数パワースペクトルにおいて音源と声道特性は和の形で表現されており,音源の特徴である基本周波数は対数パワースペクトル上の調波構造として現れることを学んだ.
ここでは,声道の特徴を考えよう.以下の図は日本語5母音の音声波形(Hanning Windowをかけたもの)とその対数パワースペクトルである.
日本語5母音では,顎の開き具合や舌の位置や唇の形などが変わることにより,声道の形が変わり,共振(共鳴)の仕方が変わる.それによって音源信号が共振され,最終的に音声が出力される.上の図から,例えば「あ」では800Hz付近と1100Hz付近が大きくなっており,「い」では300Hz付近と2100Hz付近が,「う」では300Hz付近と1100Hz付近が,「え」では400Hz付近と2000Hz付近が,「お」では400Hz付近と900Hz付近が大きくなっていることがわかる.これが声道の共振周波数を表しており,声道の形によって生じる5母音の特徴となる.
このように,声道の特徴は対数パワースペクトルの大局的な形として現れる.これをスペクトル包絡と呼び,例えば日本語5母音を認識する際などに利用できる特徴となる.
スペクトル包絡の推定
ここでは,スペクトル包絡を推定する代表的な手法として,ケプストラムを用いる方法と線形予測法(Lenear Predictive Coding: LPC)を考えよう.
ケプストラムを用いたスペクトル包絡の推定
声帯の音源信号を\(s(n)\),声道のインパルス応答を\(v(n)\)とすると,音声信号\(x(n)\)はこれらの畳込みによって表される. $$x(n)=\sum_{m=-\infty}^{\infty}s(m)v(n-m)$$ \(x(n),s(n),v(n)\)をそれぞれ離散フーリエ変換し,周波数領域で表した信号を\(X(k),S(k),V(k)\)とすると,\(X(k)\)の対数パワースペクトルは
$$\log|X(k)|^2=\log|S(k)|^2 + \log|V(k)|^2$$
となる.右辺第1項は対数パワースペクトルにおける調波構造として表現されるため,高周波成分に現れ,右辺第2項は周波数スペクトルの大局的な形(スペクトル包絡)として表されるため,低周波成分に現れる.このことから,対数パワースペクトルを1つの信号と考えると,これを離散フーリエ変換することによって得られるケプストラムに対して,高ケフレンシー成分を削除し,低ケフレンシー成分のみを離散フーリエ逆変換することにより,スペクトル包絡を求めることができる.一部の周波数成分を取り出す処理をフィルタリング(filtering)と呼ぶことをもじって,ケプストラムの一部のケフレンシー成分を取り出す処理をリフタリング(liftering)と呼ぶ.
では,日本語母音「あ」の音声に対して,ケプストラムを用いてスペクトル包絡を求めてみよう.
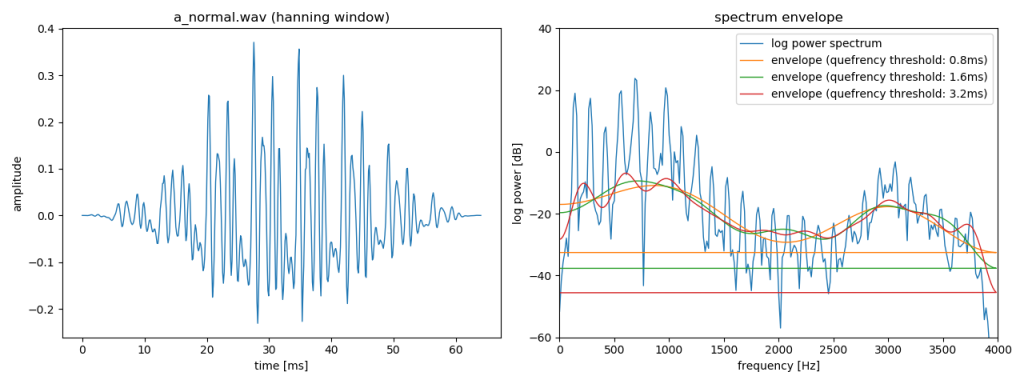
54行目までで母音「あ」の音声のケプストラムを求めている.55行目から57行目でリフタリングするケフレンシー成分のしきい値を0.8ms, 1.6ms, 3.2msとし,スペクトル包絡を求める関数calculate_log_power_spectrum_envelopeを呼び出している.この関数の定義は21行目から26行目に記述されている.22行目でケフレンシー成分のしきい値を時間から標本点のインデックス番号に変換し,23行目でケプストラムをコピーしている.24行目でしきい値以上のケフレンシー成分を0にすることで削除している.25行目で離散フーリエ逆変換をかけることで,スペクトル包絡を求めている.68行目から70行目で求めた3種類のスペクトル包絡を描画している.
実行すると,以下のように表示され,対数パワースペクトルのスペクトル包絡が求められていることがわかる.
LPCを用いた声道特性(スペクトル包絡)の推定
線形予測法(Linear Predictive Coding: LPC)とは,信号の現在の値\(x(n)\)をそれ以前の\(M\)個の値\(x(n-m), m=1,2,\cdots,M\)の線形結合によって予測するモデルである.このとき\(x(n)\)は$$x(n) = -\sum_{m=1}^{M} a_m x(n-m) + Gu(n)$$と表すことができる.ここで,\(Gu(n)\)は残差(誤差)信号とする.
\(x(n), u(n)\)の\(z\)変換をそれぞれ\(X(z), U(z)\)とすると,時間の遅れは\(z\)の次数となることから,$$X(z) = -\sum_{m=1}^{M} a_m X(z)z^{-m} + GU(z)$$となる.\(U(z)\)を線形システムへの入力,\(X(z)\)を線形システムからの出力として,それぞれを分母・分子として表現すると,$$\frac{X(z)}{U(z)} = \frac{G}{1+\sum_{m=1}^{M} a_m X(z)z^{-m}}$$となる.ここで,\(A(z) = 1+\sum_{m=1}^{M} a_m X(z)z^{-m}\)とおくと,$$\frac{X(z)}{U(z)} = \frac{G}{A(z)}$$となる.\(U(z)\)を音源信号の\(z\)変換,\(X(z)\)を音声信号の\(z\)変換とすると,声道特性\(H(z)\)は$$H(z)=\frac{X(z)}{U(z)} = \frac{G}{A(z)}$$と表せる.線形システムに対する入出力の関係として図示すると,
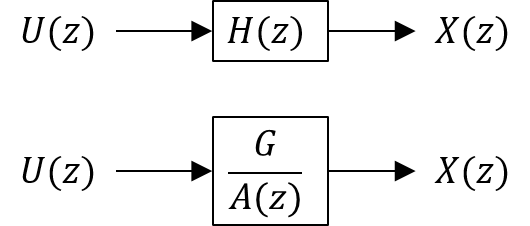
となる.
実際に声道特性を求めるには以下のようにすればよい.
- 残差\(Gu(n)\)が小さくなるようにLPC係数\(a_1,a_2,\cdots,a_M\)を推定する(ライブラリを使用することが多い).
- LPC係数の\(a_0\)を1とし,求めたいスペクトル包絡の周波数点数\(N\)の系列\(a(n) = \{a_0, a_1, \cdots, a_N\}\)をゼロ埋めによって作る.
- 系列\(a(n)\)を離散フーリエ変換し,系列\(A(k)\)を求める.
- 残差信号\(Gu(n)\)の平均として\(G\)を求める.
- 声道特性\(H(z)=\frac{G}{A(z)}\)を求める.
声道特性の対数パワースペクトルは$$20 \log_{10} |H(z)| = 20 \log_{10} |G| – 20 \log_{10} |A(z)|$$として求めることができる.
では,日本語母音「あ」の音声の声道特性(スペクトル包絡)をLPCにより求めてみよう.
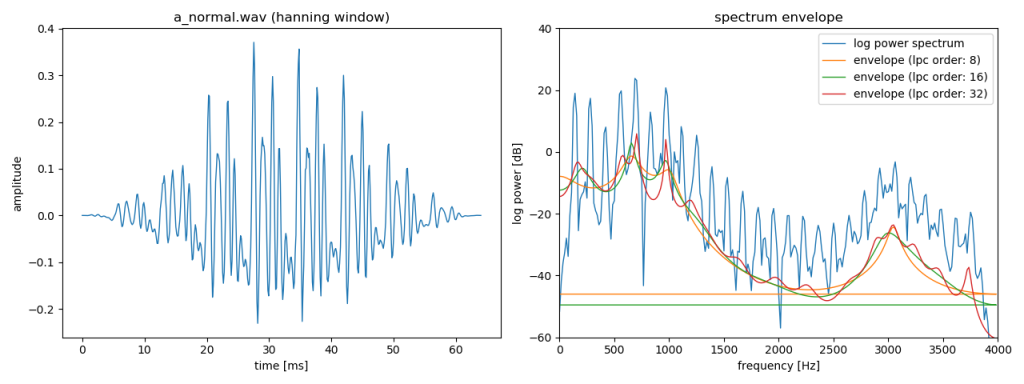
7行目でlibrosaモジュールをインポートし,56行目から58行目でlibrosaモジュールを使用して,次数(LPC係数の数)が8, 16, 32のLPC係数を求めている.59行目から61行目までで,calculate_log_power_spectrum_enverope関数を呼び出し,スペクトル包絡を求めている.この関数は23行目から28行目に定義されている.24行目でLPC係数を周波数点数を512として離散フーリエ変換している.8行目でscipyモジュールをインポートし,25行目でLPC係数によって予測される音声信号を求め,26行目で残差(誤差)の平均を求めている.27行目で声道特性の対数パワースペクトルを求めている.72行目から74行目でLPC次数を8, 16, 32として推定したスペクトル包絡を描画している.
実行すると,以下のように表示され,対数パワースペクトルのスペクトル包絡が求められていることがわかる.
日本語5母音の類似度
以上で求めたスペクトル包絡を使用して,日本語5母音の音声の類似度を測ってみよう.
ケプストラム
ケプストラムを用いてスペクトル包絡を求め,日本語5母音の類似度を求めるには以下のようにすればよい.
31行目でケフレンシーのしきい値を2msとしている.34行目から63行目で音声データのURLと保存するファイル名を指定している.67行目で各データに対して繰り返し処理をしている.65行目で空のリストを作成し,78行目でHanning Windowをかけた音声波形をリストに保存し,86行目でndarrayに変換している.66行目で空のリストを作成し,84行目でスペクトル包絡をリストに保存し,87行目でndarrayに変換している.6行目でsklernモジュールのcosine_similarityをインポートし,90行目で総当りで全ての音声波形どうしのコサイン類似度を求め,91行目で表示している.また,92行目で全ての音声のスペクトル包絡どうしのコサイン類似度を求め,93行目で表示している.
実行すると以下のように表示される.コサイン類似度とは,-1から1の間の値をとり,類似しているデータほど大きな値となる尺度である.音声波形どうしのコサイン類似度では,同じ母音の類似度が必ずしも高くなっていないことがわかる.一方,スペクトル包絡により求めたコサイン類似度では,声の高さが異なっていても同じ母音どうしで類似度が高くなっていることが確認できる.また,「あ」と「お」の類似度や「い」と「え」の類似度が高いといった特徴もうまく抽出できていることがわかる.
LPC
LPCを用いてスペクトル包絡を求め,日本語5母音の類似度を求めるには以下のようにすればよい.
33行目でLPCの次数を16としている.82行目でLPC係数を求め,83行目でスペクトル包絡を求めている.92行目で全ての組み合わせでコサイン類似度を求め,93行目で表示している.
実行すると以下のように表示され,スペクトル包絡を使用した場合,声の高さが異なっていても,同じ母音どうしで類似度が高くなっていることが確認できる.また,「あ」と「お」や「い」と「え」の類似度が高いといった特徴もうまく抽出できていることがわかる.
参考文献
- 板橋秀一,“音声工学”,森北出版,2005年2月
- 古井貞煕,“新音響・音声工学”,近代科学社,2006年9月
課題
以下の音声データを使用して課題を行え.
- 「あ」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/a_normal.wav
- 「い」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/i_normal.wav
- 「う」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/u_normal.wav
- 「え」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/e_normal.wav
- 「お」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/o_normal.wav
- 高い声で「あ」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/a_high.wav
- 低い声で「あ」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/a_low.wav
- 高い声で「い」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/i_high.wav
- 低い声で「い」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/i_low.wav
- 高い声で「う」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/u_high.wav
- 低い声で「う」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/u_low.wav
- 高い声で「え」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/e_high.wav
- 低い声で「え」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/e_low.wav
- 高い声で「お」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/o_high.wav
- 低い声で「お」と発声している音声データ
- http://makotomurakami.com/blog/wp-content/uploads/2020/05/o_low.wav
課題0
高い声と普通の声と低い声で「あ」と発声している音声データに対してケプストラムによりスペクトル包絡を求め,描画し,比較せよ.
課題1
高い声と普通の声と低い声で「い」と発声している音声データに対してケプストラムによりスペクトル包絡を求め,描画し,比較せよ.
課題2
高い声と普通の声と低い声で「う」と発声している音声データに対してケプストラムによりスペクトル包絡を求め,描画し,比較せよ.
課題3
高い声と普通の声と低い声で「え」と発声している音声データに対してケプストラムによりスペクトル包絡を求め,描画し,比較せよ.
課題4
高い声と普通の声と低い声で「お」と発声している音声データに対してケプストラムによりスペクトル包絡を求め,描画し,比較せよ.
課題5
高い声と普通の声と低い声で「あ」と発声している音声データに対してLPCによりスペクトル包絡を求め,描画し,比較せよ.
課題6
高い声と普通の声と低い声で「い」と発声している音声データに対してLPCによりスペクトル包絡を求め,描画し,比較せよ.
課題7
高い声と普通の声と低い声で「う」と発声している音声データに対してLPCによりスペクトル包絡を求め,描画し,比較せよ.
課題8
高い声と普通の声と低い声で「え」と発声している音声データに対してLPCによりスペクトル包絡を求め,描画し,比較せよ.
課題9
高い声と普通の声と低い声で「お」と発声している音声データに対してLPCによりスペクトル包絡を求め,描画し,比較せよ.

「スペクトル包絡の推定」への2件のフィードバック
コメントは受け付けていません。