目的
画像処理や音声処理といった信号処理の分野では,特定の周波数成分の信号を通過させたり遮断する処理をフィルタ処理と言う.画像に対してフィルタ処理を行うと,雑音やひずみを軽減したり,画素値が急激に変化するエッジを検出することができる.画像に対するフィルタ処理には,空間領域で表現された画像データに施す空間フィルタ処理と,画像データを離散フーリエ変換により周波数領域に変換し,周波数領域で行う周波数フィルタ処理がある.ここでは,空間フィルタ処理を学ぶ.
説明
点処理と局所処理
ここまでで学んだ表色系変換や濃度変換では,入力画像のある1つの画素に対して変換を行い,対応する出力画像の画素の値を求めた.このような処理を点処理と呼ぶ.一方,入力画像のある1つの画素とその近傍の画素から対応する出力画像の画素の値を求める処理を局所処理あるいは近傍処理と呼び,空間フィルタ処理は局所処理・近傍処理に分類される.
畳込み演算
空間フィルタ処理の一般的な処理方法は,注目画素とその近傍の画素の画素値に対してある重み付けをし,和をとり,その和を注目画素の画素値とする方法である.この重み付けに用いる値をカーネルと呼ぶ.
空間フィルタ処理の一般的な処理方法を定式化しよう.近傍領域としては3×3や5×5や7×7等が考えられる.ここでは簡単のため3×3の近傍領域における空間フィルタ処理を定式化する.今,注目画素の座標を\([x,y]\)とし,その画素値を\(f[x,y]\)とすると,3×3の近傍領域の画素値は以下のように表すことができる.
\begin{array}{|c|c|c|} \hline f[x-1,y-1] & f[x,y-1] & f[x+1,y-1] \\ \hline f[x-1,y] & f[x,y] & f[x+1,y] \\ \hline f[x-1,y+1] & f[x,y+1] & f[x+1,y+1] \\ \hline \end{array}
また,カーネルを\(w[i,j]\)とすると,3×3のカーネルは以下のように表すことができる.
\begin{array}{|c|c|c|} \hline w[-1,-1] & w[0,-1] & w[1,-1] \\ \hline w[-1,0] & w[0,0] & w[1,0] \\ \hline w[-1,1] & w[0,1] & w[1,1] \\ \hline \end{array}
近傍領域の画素値に対応するカーネルをかけて和をとったものが処理後の画素値となるので,処理後の画素値を\(f^{\prime}[x,y]\)とすると,\(f^{\prime}[x,y]\)を求める処理は以下のように定式化できる.$$f^{\prime}[x,y]=\sum_{j=-1}^{1} \sum_{i=-1}^{1} w[i,j] f[x+i,y+j] $$
これは畳込み演算と呼ばれる演算で,以下で学ぶ空間フィルタ処理の多くはこの演算によって求められる.
平滑化フィルタ
まず初めに平滑化フィルタについて学ぼう.平滑化フィルタは雑音の軽減等に使用されるので,まず画像データに人工的に雑音をのせる方法を考えよう.人工的な雑音の代表的なものにはごま塩雑音とガウシアンノイズがある.
ごま塩雑音
ごま塩雑音とは,白(塩)と黒(ごま)の画素をある確率でランダムな位置にのせることによって生成できる雑音である.画像にごま塩雑音をのせるには,以下のようにすればよい.
23行目でカラー画像を読み込み,25行目から27行目でコマンドライン引数で指定された場合にグレースケール画像に変換している.29行目で乱数生成器を作り,30行目で変換前の画像をコピーしている.32行目でコマンドライン引数で指定した確率で乱数を生成し,この乱数が示すインデックス番号の画素に白のノイズをのせることにする.33,34行目でインデックス番号をy座標とx座標に変換し,35行目から38行目でその位置の画素を白にしている.同様に,40行目から46行目で黒のノイズをのせている.
コマンドライン引数の指定を変えて実行すると,以下のような画像が出力される.以下は,カラー画像・グレースケール画像に対して,白黒ともに0.01の確率で生成したごま塩雑音をのせた画像と,白黒ともに0.02の確率で生成したごま塩雑音をのせた画像である.
ガウシアンノイズ
ガウシアンノイズは正規分布(ガウス分布)に基づいて画素値を変更することによって生成できる雑音である.画像にガウシアンノイズをのせるには,以下のようにすればよい.
31行目でコマンドライン引数で指定した標準偏差で平均0の正規分布から画素値の数だけ乱数を生成し,32行目から35行目で画像データのshapeと同じになるようにreshapeしている.36行目で生成した乱数だけ画素値を変更し,37行目から39行目で後処理をしている.
コマンドライン引数の指定を変えて実行すると,以下のような画像が出力される.以下は,カラー画像・グレースケール画像に対して,標準偏差20で生成したガウシアンノイズをのせた画像と,標準偏差40で生成したガウシアンノイズをのせた画像である.

平均値フィルタ(3×3)
雑音軽減等に使用される平滑化フィルタの代表的なものに平均値フィルタがある.平均値フィルタでは,注目画素と近傍画素の画素値の平均を注目画素の処理後の画素値とする.例えばごま塩雑音に対して近傍画素との平均をとると雑音が軽減されることから,雑音を軽減する目的で使用される.以下に示すような3×3のカーネルを使用して畳込み演算を行うと3×3の近傍領域の平均が計算できることから,実際の計算には畳込み演算が使用されることが多い.
\begin{array}{|c|c|c|} \hline \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \\ \hline \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \\ \hline \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \\ \hline \end{array}
画像に対して3×3の平均値フィルタをかけるには,以下のようにすればよい.
11行目で画像を読み込み,13行目から15行目で3×3の平均値フィルタのカーネルを作り,16行目で畳込み演算を行っている.ごま塩雑音がのったカラー画像・グレースケール画像に3×3の平均値フィルタをかけた結果は以下のようになる.
平均値フィルタ(3×3, 中央の重みが2倍)
以上の例では,中央の画素値にも近傍の8画素の画素値にも同じ重みを使用していたが,中央の画素は近傍の画素よりも重要であると考え,中央の重みを大きくすることもできる.例えば,中央の重みを近傍の2倍にすると,カーネルは以下のようになる.分母が10となっているのは,カーネルの値の和が1となるようにし,全体の明るさが変化しないようにするためである.
\begin{array}{|c|c|c|} \hline \frac{1}{10} & \frac{1}{10} & \frac{1}{10} \\ \hline \frac{1}{10} & \frac{2}{10} & \frac{1}{10} \\ \hline \frac{1}{10} & \frac{1}{10} & \frac{1}{10} \\ \hline \end{array}
画像に対して中央の重みが2倍の3×3の平均値フィルタをかけるには,以下のようにすればよい.
ごま塩雑音がのったカラー画像・グレースケール画像に中央の重みが2倍の3×3の平均値フィルタをかけた結果は以下のようになる.
平均値フィルタ(5×5)
近傍領域が5×5の平均値フィルタのカーネルは以下のようになる.
\begin{array}{|c|c|c|c|c|} \hline \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \\ \hline \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \\ \hline \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \\ \hline \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \\ \hline \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \\ \hline\end{array}
画像に対して5×5の平均値フィルタをかけるには,以下のようにすればよい.
ごま塩雑音がのったカラー画像・グレースケール画像に5×5の平均値フィルタをかけた結果は以下のようになる.
平均値フィルタ(関数)
OpenCVでは,以上のようにカーネルを指定して畳込み演算を行う他に,平均値フィルタをかけるための関数が用意されている.関数を使用して平均値フィルタをかけるには以下のようにすればよい.
12,13行目のようにカーネルサイズを指定してblur関数を呼び出すと平均値フィルタをかけることができる.また,14,15行目のようにboxFilter関数を呼び出しても平均値フィルタをかけることができる.
ガウシアンフィルタ
以上では,近傍画素の平均をとって画像を平滑化した.近傍画素の平均の代わりに,正規分布(ガウス分布)にしたがうカーネルを用いて畳込み演算を行うことで平滑化を行うフィルタをガウシアンフィルタと呼ぶ.平均が\(\mu\),標準偏差が\(\sigma\)の正規分布は以下のように表すことができる.$$f(x,y) = \frac{1
}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^2}{2 {\sigma}^2} \right)$$
画像に対してガウシアンフィルタをかけるには以下のようにすればよい.
13行目でカーネルサイズが5,標準偏差が3,平均が0の1次元ガウシアンカーネルを求め,15行目で表示している.14行目で1次元ガウシアンカーネルの外積を計算することで2次元のガウシアンカーネルを求め,16行目で表示している.実行すると以下のように表示され,1次元・2次元のサイズが5のガウシアンカーネルが表示される.
17行目でガウシアンカーネルを用いて畳込み演算を行い,20行目で表示している.ごま塩雑音がのったカラー画像・グレースケール画像に5×5の標準偏差が3のガウシアンフィルタをかけた結果は以下のようになる.
ガウシアンフィルタ(関数)
OpenCVでは,ガウシアンカーネルを指定して畳込み演算を行う他に,ガウシアンフィルタをかけるための関数が用意されている.関数を使用してガウシアンフィルタをかけるには以下のようにすればよい.
11行目のように,カーネルサイズとx方向とy方向の標準偏差を指定してGaussianBlur関数を呼び出すと,ガウシアンフィルタをかけることができる.
メディアンフィルタ
メディアン(中央値)フィルタでは,注目画素と近傍画素の画素値の中央値を注目画素の処理後の画素値とする.例えばごま塩雑音に対して近傍画素との中央値とると,ほとんどの箇所で雑音を除去することができる.
画像に対して3×3のメディアンフィルタをかけるには,以下のようにすればよい.
11行目で3×3のメディアンフィルタをかけ,14行目で表示している.ごま塩雑音がのったカラー画像・グレースケール画像に3×3のメディアンフィルタをかけた結果は以下のようになる.
1次微分フィルタ
画像の解析は,画像のもつ2次元的な特徴を抽出することによって行われることが多い.輝度や色などの特徴が似ている部分を1つの領域と考えたときに,領域と領域の境界では特徴が急激に変化する.この境界のことをエッジと呼び,エッジは画像の解析によく使用される特徴の1つである.
方法0
画像からエッジを検出するには,画像の微分が利用される.画像データは\(x, y\)の2つの変数に対する関数\(f[x,y]\)として表現されたので,画像を微分する際には,\(f\)を\(x\)のみの関数とみなして微分するか,\(f\)を\(y\)のみの関数とみなして微分することになる.これを偏微分と呼ぶ.\(x\)方向の偏微分は\(x\)が少し変化したときの\(f\)の変化量となるので,例えば,今注目している画素\([x,y]\)と右隣の画素\([x+1,y]\)を使うと,以下のように表すことができる.
$$\frac{\partial f}{\partial x}=\frac{f[x+1,y]-f[x,y]}{x+1-x}=f[x+1,y]-f[x,y]$$
\(y\)方向の偏微分も同様に,今注目している画素\([x,y]\)と1つ下の画素\([x,y+1]\)を使うと,以下のように表すことができる.
$$\frac{\partial f}{\partial y}=\frac{f[x,y+1]-f[x,y]}{y+1-y}=f[x,y+1]-f[x,y]$$
\(\frac{\partial f}{\partial x}\)を3×3のカーネルで表現すると,以下のようになり,
\begin{array}{|c|c|c|} \hline 0 & 0 & 0 \\ \hline 0 & -1 & 1 \\ \hline 0 & 0 & 0 \\ \hline \end{array}
\(\frac{\partial f}{\partial y}\)を3×3のカーネルで表現すると,以下のようになる.
\begin{array}{|c|c|c|} \hline 0 & 0 & 0 \\ \hline 0 & -1 & 0 \\ \hline 0 & 1 & 0 \\ \hline \end{array}
方法1
以上の方法では,\(x\)方向に対する\(f\)の勾配を求める際に,右隣の画素から注目画素の画素値を引いている.また,\(y\)方向に対する\(f\)の勾配を求める際には,1つ下の画素から注目画素の画素値を引いている.このように求める場合,正確には注目画素よりも右に\(\frac{1}{2}\),下に\(\frac{1}{2}\)だけずれた点の勾配を求めていることになる.対称性をもたせたければ,\(x\)方向に対する\(f\)の勾配を求める際に,右隣の画素から左隣の画素の画素値を引けばよいだろう.また,\(y\)方向に対する\(f\)の勾配を求める際には,1つ下の画素から1つ上の画素の画素値を引けばよいだろう.
$$\frac{\partial f}{\partial x}=f[x+1,y]-f[x-1,y]$$
$$\frac{\partial f}{\partial x}=f[x,y+1]-f[x,y-1]$$
\(\frac{\partial f}{\partial x}\)を3×3のカーネルで表現すると,以下のようになり,
\begin{array}{|c|c|c|} \hline 0 & 0 & 0 \\ \hline -1 & 0 & 1 \\ \hline 0 & 0 & 0 \\ \hline \end{array}
\(\frac{\partial f}{\partial y}\)を3×3のカーネルで表現すると,以下のようになる.
\begin{array}{|c|c|c|} \hline 0 & -1 & 0 \\ \hline 0 & 0 & 0 \\ \hline 0 & 1 & 0 \\ \hline \end{array}
勾配ベクトル
いずれの方法でも,\(f\)の\(x\)方向の勾配と\(y\)方向の勾配が求められた.これらを並べて1つのベクトルとして表したものを勾配ベクトルと呼ぶ.
$$\nabla f = \left [ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right ]$$
直交座標で表現された勾配ベクトルを極座標で表すと,勾配の大きさと勾配の方向が求められる.
$$|\nabla f| = \sqrt{ \left ( \frac{\partial f}{\partial x} \right )^2 + \left ( \frac{\partial f}{\partial y} \right )^2 }$$
$$\angle (\nabla f) = \tan^{-1} \left ( \frac{\frac{\partial f}{\partial x}}{\frac{\partial f}{\partial y}} \right ) $$
エッジ検出(方法0)
画像に対し,方法0でエッジ検出を行うには以下のようにすればよい.
28行目でカラー画像を読み込み,29行目でグレースケール画像に変換している.31行目から38行目で,\(f\)の\(x\)方向の勾配と\(y\)方向の勾配を求め,39行目で勾配の大きさを求めている.これらの値が大きいほど白,小さいほど黒とし,8bitグレースケール画像として出力するには,各値が0から255の間の値となるように線形濃度変換すればよい.8行目から13行目に線形濃度変換する関数を定義し,40行目から42行目でこの関数を呼び出し,\(x\)方向の勾配,\(y\)方向の勾配,勾配の大きさのそれぞれを8bitグレースケール画像に変換している.実行すると以下のように表示され,勾配の大きさとしてエッジが検出できていることがわかる.
エッジ検出(方法1)
画像に対し,方法1でエッジ検出を行うには以下のようにすればよい.
31行目から38行目で,\(f\)の\(x\)方向の勾配と\(y\)方向の勾配を求め,39行目で勾配の大きさを求めている.実行すると以下のように表示され,勾配の大きさとしてエッジが検出されていることがわかる.
ここまでで2種類の1次微分フィルタを学んだが,その他に名前がついている1次微分フィルタが3種類ある.ここからは,Robertsフィルタ,Prewittフィルタ,Sobelフィルタと呼ばれる1次微分フィルタについて学ぶ.
Robertsフィルタ
Robertsフィルタでは,\(f\)の\(x\)方向の勾配を求める際に注目画素から右下の画素値を引く.また,\(f\)の\(y\)方向の勾配を求める際には1つ下の画素から1つ右の画素の画素値を引く.このことから,Robertsフィルタは斜め方向の画素値の差を利用した1次微分フィルタとなる.
$$\frac{\partial f}{\partial x}=f[x,y]-f[x+1,y+1]$$
$$\frac{\partial f}{\partial x}=f[x,y+1]-f[x+1,y]$$
\(\frac{\partial f}{\partial x}\)を3×3のカーネルで表現すると,以下のようになり,
\begin{array}{|c|c|c|} \hline 0 & 0 & 0 \\ \hline 0 & 1 & 0 \\ \hline 0 & 0 & -1 \\ \hline \end{array}
\(\frac{\partial f}{\partial y}\)を3×3のカーネルで表現すると,以下のようになる.
\begin{array}{|c|c|c|} \hline 0 & 0 & 0 \\ \hline 0 & 0 & -1 \\ \hline 0 & 1 & 0 \\ \hline \end{array}
画像にRobertsフィルタをかけ,エッジ検出を行うには以下のようにすればよい.
31行目から38行目で,\(f\)の\(x\)方向の勾配と\(y\)方向の勾配を求め,39行目で勾配の大きさを求めている.実行すると以下のように表示され,勾配の大きさとしてエッジが検出されていることがわかる.
Prewittフィルタ
ここまでで学んだ3種類の1次微分フィルタはいずれも2画素間の差分を用いていた.そのため,注目画素に雑音がのっていると安定したエッジ検出ができないという欠点がある.勾配ベクトルを求める際に注目画素の近傍画素も使用すれば,注目画素に雑音がのっている場合でも安定したエッジ検出ができる.そこで,\(f\)の\(x\)方向の勾配を求める際に,注目画素の左右の画素値の差に加えて,上下の行における左右の画素値の差,すなわち注目画素の左上と右上の画素値の差と注目画素の左下と右下の画素値の差を求め,和をとる.この処理をカーネルを用いて表現すると以下のようになる.
\begin{array}{|c|c|c|} \hline -1 & 0 & 1 \\ \hline -1 & 0 & 1 \\ \hline -1 & 0 & 1 \\ \hline \end{array}
同様に,\(f\)の\(y\)方向の勾配を近傍領域に拡張して求める処理は,以下のようなカーネルにより表現できる.
\begin{array}{|c|c|c|} \hline -1 & -1 & -1 \\ \hline 0 & 0 & 0 \\ \hline 1 & 1 & 1 \\ \hline \end{array}
このように近傍領域に拡張した1次微分フィルタをPrewittフィルタと呼ぶ.
画像にPrewittフィルタをかけ,エッジ検出を行うには以下のようにすればよい.
31行目から38行目で,\(f\)の\(x\)方向の勾配と\(y\)方向の勾配を求め,39行目で勾配の大きさを求めている.実行すると以下のように表示され,勾配の大きさとしてエッジが検出されていることがわかる.
Sobelフィルタ
Prewittフィルタで勾配ベクトルを求める際には,注目画素における勾配を近傍画素における勾配と同じ重みで求めていた.注目画素における勾配は近傍画素における勾配よりも重要だと考えるのであれば,注目画素に対する重みを大きくすればよいだろう.近傍画素における勾配に対して注目画素における勾配の重みを2倍にすると,\(f\)の\(x\)方向の勾配を求めるカーネルは以下のように表すことができる.
\begin{array}{|c|c|c|} \hline -1 & 0 & 1 \\ \hline -2 & 0 & 2 \\ \hline -1 & 0 & 1 \\ \hline \end{array}
また,\(f\)の\(y\)方向の勾配を求めるカーネルは以下のように表すことができる.
\begin{array}{|c|c|c|} \hline -1 & -2 & -1 \\ \hline 0 & 0 & 0 \\ \hline 1 & 2 & 1 \\ \hline \end{array}
このようにPrewittフィルタの中央の重みを2倍にした1次微分フィルタをSobelフィルタと呼ぶ.
画像にSobelフィルタをかけ,エッジ検出を行うには以下のようにすればよい.
31行目から38行目で,\(f\)の\(x\)方向の勾配と\(y\)方向の勾配を求め,39行目で勾配の大きさを求めている.実行すると以下のように表示され,勾配の大きさとしてエッジが検出されていることがわかる.
Sobelフィルタ(カーネルを関数で求める)
以上の例ではカーネルを指定して画像に3×3のSobelフィルタをかけた.OpenCVにはSobelフィルタのカーネルを求める関数が用意されており,この関数を使用すれば,サイズが大きいSobelフィルタのカーネルを求めることができる.画像に3×3と5×5のSobelフィルタをかけるには,以下のようにすればよい.
31,32行目のように記述すると,カーネルサイズが3×3の\(x\)方向の勾配を求めるSobelフィルタのカーネルを求めることができる.同様に33,34行目のように記述すると,3×3の\(y\)方向の勾配を求めるSobelフィルタのカーネルを求めることができる.また,44行目から47行目のように記述すると,カーネルサイズが5×5の\(x, y\)方向の勾配を求めるSobelフィルタのカーネルを求めることができる.35,36,48,49行目で求めたカーネルを表示している.実行すると以下のように表示され,3×3, 5×5のSobelフィルタのカーネルが表示されていることがわかる.
5×5のSobelフィルタによって求められた\(f\)の\(x\)方向の勾配と\(y\)方向の勾配と勾配の大きさは以下のようになり,勾配の大きさとしてエッジが検出されていることがわかる.
Sobelフィルタ(関数)
OpenCVにはSobelフィルタにより勾配ベクトルを求める関数が用意されている.この関数を使用して画像にSobelフィルタをかけてみよう.
31行目のように記述すると,カーネルサイズが3×3のSobelフィルタにより画像の\(x\)方向の勾配を求めることができる.同様に32行目のように記述すると,3×3のSobelフィルタにより画像の\(y\)方向の勾配を求めることができる.また,38,39行目のように記述すると,カーネルサイズが5×5のSobelフィルタにより画像の\(x,y\)方向の勾配を求めることができる.
2次微分フィルタ
ラプラシアン
画像データは\(x,y\)の2つの変数に対する関数\(f\)として表現された.そのため画像を微分する際には\(x,y\)それぞれの方向に偏微分することになる.画像の1次微分では\(x,y\)それぞれの方向に1度偏微分したものをベクトルとして表現し,勾配ベクトル$$\nabla f = \left [ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right ]$$を求めた.画像の2次微分では\(x,y\)それぞれの方向に2度偏微分したものの和$$\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}$$を求める.これをラプラシアンと呼ぶ.
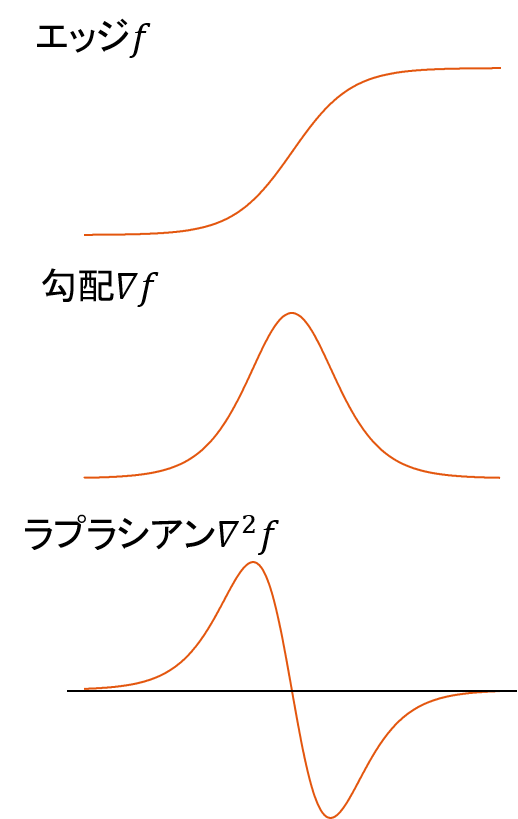
今,輝度値が図のように変化するエッジがあったとする.このとき,輝度値の勾配は0から大きくなり,中央の辺りで最大となった後,小さくなり,0になる.ラプラシアンは勾配の勾配になるので,同様に考えると,左の領域と中央と右の領域で0となる.勾配が一番急峻な中央やや左で正の最大値,中央やや右で負の方向に最大値(最小値)をとり,全体としては図のように変化する.エッジとラプラシアンを比較すると,ラプラシアンはエッジの下端で正のピーク,上端で負のピークをもち,正負のピークの中央で0となることがわかる.
では,ディジタル画像のラプラシアンを求める方法を考えよう.\(x\)方向の2次偏微分では,\(x\)方向に偏微分したものをもう1度\(x\)方向に偏微分すればよい.
\begin{eqnarray} \frac{\partial^2 f}{\partial x^2} &=& \frac{\partial}{\partial x}(f[x+1,y]-f[x,y]) \\ &=& (f[x+1,y]-f[x,y]) – (f[x,y]-f[x-1,y]) \\ &=& f[x+1,y] + f[x-1,y] – 2f[x,y] \end{eqnarray}
\(y\)方向の2次偏微分も同様に求めると,
\begin{eqnarray} \frac{\partial^2 f}{\partial y^2} &=& \frac{\partial}{\partial y}(f[x,y+1]-f[x,y]) \\ &=& (f[x,y+1]-f[x,y]) – (f[x,y]-f[x,y-1]) \\ &=& f[x,y+1] + f[x,y-1] – 2f[x,y] \end{eqnarray}
となる.ラプラシアンはこれらの和であるから
\begin{eqnarray} \nabla^2 f &=& \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} \\ &=& f[x+1,y] + f[x-1,y] + f[x,y+1] + f[x,y-1] – 4f[x,y] \end{eqnarray}
となり,カーネルを使用して表すと
\begin{array}{|c|c|c|} \hline 0 & 1 & 0 \\ \hline 1 & -4 & 1 \\ \hline 0 & 1 & 0 \\ \hline \end{array}
となる.
画像に対してラプラシアンフィルタをかけるには,以下のようにすればよい.
33行目でラプラシアンフィルタのカーネルを作成し,36行目で畳込み演算を行い,37行目で結果の画像データを作成している.カラー画像・グレースケール画像にラプラシアンフィルタをかけた結果は以下のようになる.
鮮鋭化
ラプラシアンの応用例として鮮鋭化について考えよう.鮮鋭化とは画像改善の一種で,ピンぼけした画像をくっきりはっきり補正する処理である.ピンぼけした画像のエッジでは図のように輝度値の変化が緩やかなってしまっている.これを急峻となるように変換する処理が鮮鋭化になる.

既に説明したように,図のようなぼけたエッジがあったときに,勾配とラプラシアンは図のようになる.また,ラプラシアンは,エッジの下端で正のピーク,上端で負のピークをもち,正負のピークの中央で0になった.そのラプラシアンを上下反転させると,図のようになり,エッジの下端で負のピーク,上端で正のピークをもち,正負のピークの中央で0となる.したがって,元の画像からラプラシアンを引くと,エッジの下端の値が小さくなり,エッジの上端の値が大きくなるため,図のように緩やかなエッジを急峻にすることができる.

以上のように入力画像からラプラシアンを引けば鮮鋭化ができる.したがって鮮鋭化の処理は
\begin{eqnarray} f^{\prime}[x,y] &=& f[x,y] – \nabla^2 f \\ &=& f[x,y] – (f[x+1,y] + f[x-1,y] + f[x,y+1] + f[x,y-1] – 4f[x,y]) \\ &=& 5f[x,y] – f[x+1,y] – f[x-1,y] – f[x,y+1] – f[x,y-1]\end{eqnarray}
となり,これをカーネルを使用して表すと
\begin{array}{|c|c|c|} \hline 0 & -1 & 0 \\ \hline -1 & 5 & -1 \\ \hline 0 & -1 & 0 \\ \hline \end{array}
となる.
画像に対して鮮鋭化処理をするには,以下のようにすればよい.
25行目で鮮鋭化フィルタのカーネルを作成し,28行目で畳込み演算を行い,29,30行目で後処理を行っている.カラー画像・グレースケール画像を鮮鋭化した結果は以下のようになり,細かい文字等が鮮鋭化されていることが確認できる.
ラプラシアン(関数)
OpenCVにはラプラシアンを求める関数が用意されている.関数により画像にラプラシアンフィルタをかけるには以下のようにすればよい.
33行目のように記述することで画像にラプラシアンフィルタをかけることができる.
課題
課題0
画像を読み込み,3×3の平均値フィルタにより平滑化せよ.
課題1
画像を読み込み,5×5の平均値フィルタにより平滑化せよ.
課題2
画像を読み込み,標準偏差3の5×5のガウシアンフィルタにより平滑化せよ.
課題3
画像を読み込み,3×3のメディアンフィルタにより平滑化せよ.
課題4
画像を読み込み,Robertsフィルタによりエッジ検出せよ.
課題5
画像を読み込み,Prewittフィルタによりエッジ検出せよ.
課題6
画像を読み込み,3×3のSobelフィルタによりエッジ検出せよ.
課題7
画像を読み込み,5×5のSobelフィルタによりエッジ検出せよ.
課題8
画像を読み込み,ラプラシアンフィルタをかけよ.
課題9
画像を読み込み,鮮鋭化せよ.













