離散フーリエ変換

目的

音声を処理する際に，離散フーリエ変換をかけ，時間領域から周波数領域に変換することがある．ここでは，正弦波を重ね合わせた信号に対して離散フーリエ変換をかける方法を学ぶ．

説明

音声データに対して処理をする前に，ここでは正弦波を重ね合わせた信号を処理することを考える．まず，正弦波を3つ重ね合わせた信号を作ってみよう．

正弦波の重ね合わせ

正弦波・余弦波

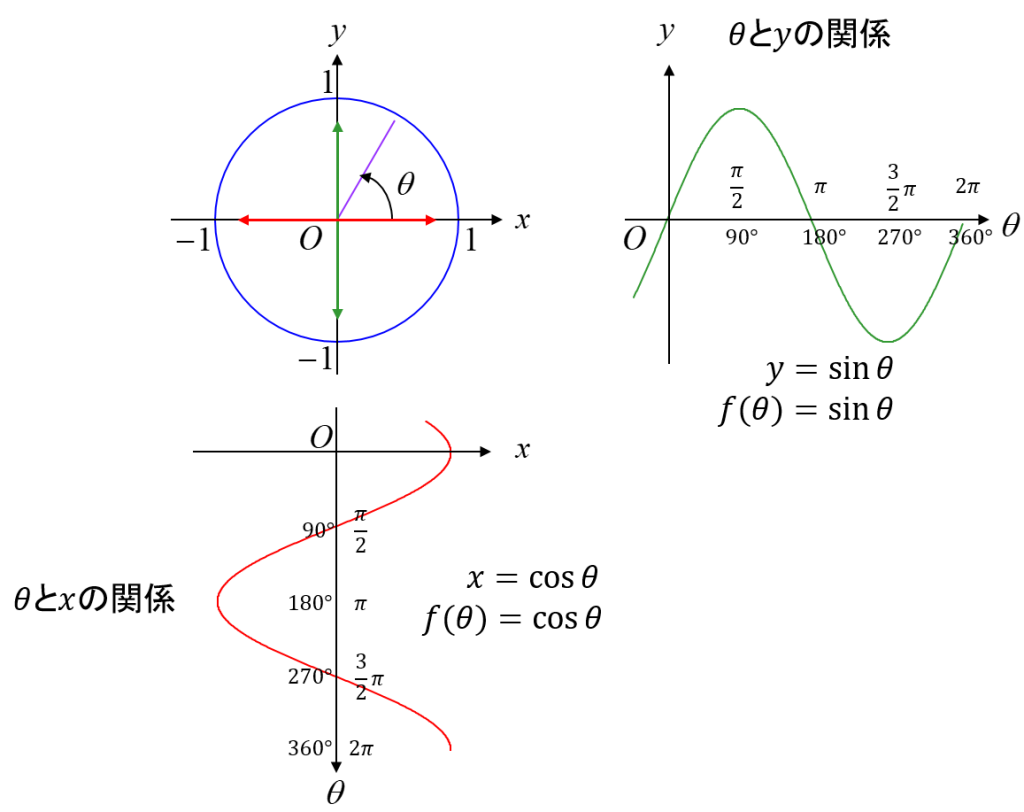
原点$O$を中心とし半径が1の単位円があるとする．偏角$\theta$と単位円上の点の$y$座標との関係が正弦関数であり，$y=\sin \theta$と表現する．同様に，偏角$\theta$と単位円上の点の$x$座標との関係が余弦関数であり，$x=\cos \theta$と表現する．

時間関数

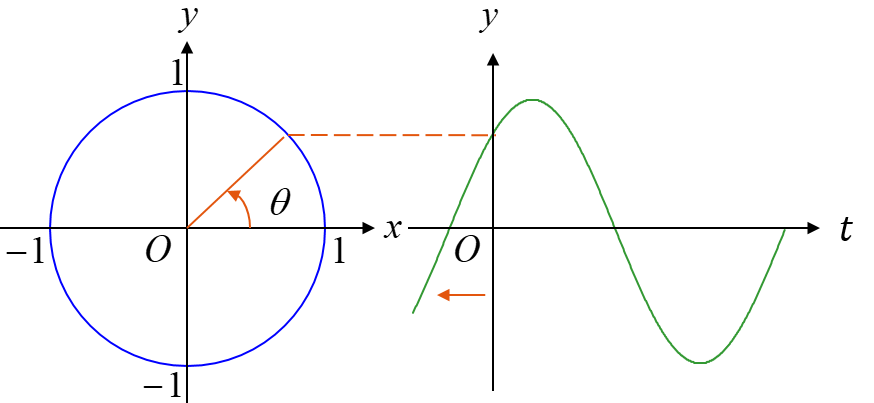
正弦関数$y=\sin \theta$は角度$\theta$の関数であるが，音声信号は時間$t$の関数である．角度$\theta$の関数を時間$t$の関数に変換してみよう．時間$t$と角度$\theta$と角速度$\omega$の関係は，時間$t$と距離$x$と速度$v$と同様であり，$\theta = \omega t$となる．この関係を利用すると，正弦関数は$$y=\sin \omega t$$と書き換えることができる．$t$を変数，$\omega$を定数と考えれば，時間$t$の関数として表されていることがわかる．

角速度・周期・周波数

正弦関数は周期関数であるが，元に戻って繰り返すのにかかる時間（単位は[s]）を周期$T$と呼び，1秒間に繰り返す（振動する）回数（単位は[Hz]）を周波数と呼ぶ．

例えば角速度$\omega$が毎秒$\frac{\pi}{2}$ラジアン（90度）とすると，4秒で1度振動する（360度回転する）ことから，周期$T$は4秒であり，4秒で1度振動することから，1秒で$\frac{1}{4}$回振動すると考え，周波数$f$は$\frac{1}{4}$Hzとなる．同様に，角速度$\omega$が毎秒$\pi$ラジアン（180度）とすると，周期$T$は2秒であり，周波数$f$は$\frac{1}{2}$Hzとなる．以上の例から，角速度$\omega$，周期$T$，周波数$f$との間には以下のような関係があることがわかる．

$$\omega T = 2 \pi \\ \omega = 2 \pi f \\ fT =1$$

以上の関係より，正弦関数を角速度$\omega$ではなく周波数$f$で表すと，$$y=\sin 2 \pi f t$$となる．また，角速度$\omega$，周期$T$，周波数$f$は正弦波の横方向の縮尺を制御するパラメータだと考えることができる．

振幅

正弦波の縦方向の縮尺を変更してみよう．正弦関数は-1から1の間で振動するが，振動の幅を変更するには，振幅$A$をかければよい．$$y=A \sin 2 \pi f t$$

位相

正弦関数は時間$t=0$のとき，$y=0$となるが，時刻$t=0$のときに角度が$\theta$となるようにすると，その分だけ正弦波を横方向にシフトすることができる．$$y=A \sin (2 \pi f t + \theta)$$

離散時間信号

以上では連続時間信号を考えたが，コンピュータで信号を扱う際に連続の時間を表現することができないため，時間方向に離散化する必要がある．時間的に連続な信号を適当な時間間隔で離散化して取り出す操作を標本化と呼び，信号を取り出す時間間隔（単位は[s]）を標本化周期$T_s$，1秒間に取り出す標本点の数（単位は[Hz]）を標本化周波数$f_s$と呼ぶ．標本化周期と標本化周波数の間には逆数の関係（$f_s T_s = 1$）がある．

正弦波の重ね合わせ

振幅・周波数・位相が異なる3種類の正弦波を重ね合わせてできる波を表示するには，以下のようにすればよい．

6行目から8行目で，標本点を512，標本化周波数を8kHzとし，トータルの時間を求めている．10行目で各標本点の時間からなるリストを生成している（後でグラフを描くときの横軸として使用するため）．

12行目から14行目で1つ目の正弦波のパラメータ（振幅3，周波数400Hz, 位相(\frac{\pi}{6})ラジアン）を設定している．同様に15行目から17行目で2つ目の正弦波のパラメータを，18行目から20行目で3つ目の正弦波のパラメータを設定している． 21行目から23行目で振幅・周波数・位相が異なる3つの正弦波を重ね合わせてできる波を作っている．

25行目から31行目で3つの正弦波を重ね合わせた波を表示している．

実行すると，以下のような信号が表示される．

窓関数

音声データは短時間で区切って処理することが多く，元のデータから短時間のデータを取り出すときに窓関数をかけることが多い．代表的な窓関数としては以下のものがある．式中の$N$は標本点の数とする．

Hamming Window

$$w(n) = 0.54 – 0.46 \cos \frac{2 \pi n}{N-1}, 0 \leq n \leq N-1$$

Hanning Window

$$w(n) = 0.5 – 0.5 \cos \frac{2 \pi n}{N-1}, 0 \leq n \leq N-1$$

Blackman Window

$$w(n) = 0.42 – 0.5 \cos \frac{2 \pi n}{N} + 0.08 \cos \frac{4 \pi n}{N}, 0 \leq n \leq N-1$$

Bartlett Window

$$w(n) = \frac{2}{N-1} (\frac{N-1}{2} – |n-\frac{N-1}{2} |), 0 \leq n \leq N-1$$

Kaiser Window

$$w(n) = \frac{I_0(\beta \sqrt{1-\frac{4n^2}{(N-1)^2}})}{I_0(\beta)},- \frac{N-1}{2} \leq n \leq \frac{N-1}{2}$$

ここで，$I_0$はnormalized zoroth-order Bassel functionと呼ばれる関数である．Kaiser Windowは，以下のようにパラメータ$\beta$の値を変更すると，その他の窓関数に似るように設計されている．

$\beta=0$のとき，Rectangular Window
$\beta=5$のとき，Hamming Window
$\beta=6$のとき，Hanning Window
$\beta=8.6$のとき，Blackman Window

窓関数の描画

各窓関数を描画するには以下のようにすればよい．

6行目で標本点の数を512とし，8行目から11行目までで標本点512点のHamming, Hanning, Blackman, Bartlett Windowを生成している．12行目から15行目までで標本点512点のKaiser Windowをパラメータ$\beta$の値を0, 5, 6, 8.6と変更して生成している．17行目から60行目でそれぞれの窓関数を描画している．

実行すると，以下のように窓関数が表示される．

正弦波からなる信号に窓関数をかける

3つの正弦波からなる信号に窓関数をかけてみよう．

25行目から29行目で5種類の窓関数を3つの正弦波を重ね合わせて作った信号にかけている．31行目から76行目で窓関数をかけない（方形窓をかけた）信号と5種類の窓関数をかけた信号を表示すると，以下のように表示される．

元の信号を$x(n), 0 \leq n \leq N-1$，離散フーリエ変換により周波数領域に変換された信号を$X(k), 0 \leq k \leq N-1$とすると，離散フーリエ変換は以下のようになる．$$X(k) = \sum_{n=0}^{N-1} x(n) e^{-j \frac{2 \pi kn}{N}}$$

離散フーリエ変換によって得られた信号$X(k)$は複素数であり，絶対値をとった値$|X(k)|$は実数値となる．これを振幅と呼び，横軸に周波数縦軸に振幅をプロットしたグラフを振幅スペクトルと呼ぶ．振幅スペクトルは周波数$f=0$に対して線対称になり，離散フーリエ変換によって得られた振幅スペクトルは周期性を持つという性質があるため，実際には得られたデータの半分だけを描画することが多い．

離散フーリエ変換を高速に計算することができる高速フーリエ変換というアルゴリズムが提案されており，実際にはライブラリを使用して変換することが多い．ここでは，numpyを使用して高速フーリエ変換を行い，周波数スペクトルを表示してみよう．

31行目から36行目で，窓関数をかけない信号と5種類の窓関数をかけた信号に対して高速フーリエ変換を行い，周波数領域の信号を求めている．38行目から43行目で絶対値をとるにより振幅を求めている．45行目で周波数ポイント数と標本化周期から，グラフの横軸である周波数のデータを生成している．91行目から131行目で，6種類の信号の振幅スペクトルを描画している．93行目のように記述することで，横軸を半分だけ表示するようにしている．

実行すると，以下のように6種類の信号の振幅スペクトルが表示される．

元の信号は周波数が400Hz, 1200Hz, 3000Hzであり，正しく周波数成分が求められていることがわかる．また，それぞれの振幅の比が3:2:1と正しく求められていることも確認できる．

窓関数をかけない場合の振幅スペクトルの裾野が窓関数をかけた信号の振幅スペクトルよりも広がっていることがわかる．離散フーリエ変換では元の信号が周期的であることを仮定しているが，窓関数をかけないと信号の左端と右端が滑らかに接続されないため，周期性の仮定が崩れてしまうためにこのようなことが起こる．そこで左右になるほど値が小さくなるような窓関数をかけることにより，信号の左端と右端が滑らかに接続され，周期性のある波に近づけることができ，振幅スペクトルを実際の周波数成分に近い形で求めることができる．

離散フーリエ逆変換

周波数領域で表現された信号$X(k)$に離散フーリエ逆変換をかけると，時間領域で表現された信号$x(n)$を求めることができる．$$x(n) = \frac{1}{N} \sum_{k=0}^{N-1} X(k) e^{j \frac{2 \pi kn}{N}}$$離散フーリエ逆変換もライブラリを使用して高速フーリエ逆変換として変換することが多い．

47行目から52行目で高速フーリエ逆変換を行っている．逆変換した結果は複素数であるが，実数成分が元の信号を表しているため「.real」として実数成分を取り出している．140行目から174行目で逆変換した信号を描画している．

実行すると以下のようになり，元の時間信号が求められていることがわかる．

課題

課題0

周波数400Hz・振幅8・位相$\pi$ラジアン，周波数600Hz・振幅6・位相$\frac{\pi}{2}$ラジアン，周波数1400Hz・振幅4・位相$-\frac{\pi}{3}$ラジアン，周波数2600Hz・振幅2・位相$-\frac{\pi}{4}$ラジアン，周波数3200Hz・振幅1・位相$\frac{\pi}{6}$ラジアンの正弦波からなる信号を作り，表示せよ．標本点の数は512点，標本化周波数は8kHzとせよ．

課題1

課題0の信号に方形窓をかけ（窓関数をかけずに）離散フーリエ変換を行い，振幅スペクトルを表示せよ．また，離散フーリエ逆変換を行い，求められた信号を表示せよ．

課題2

課題0の信号にHamming Windowをかけた信号を表示せよ．その信号に対して離散フーリエ変換を行い，振幅スペクトルを表示し，課題1の結果と比較せよ．また，離散フーリエ逆変換を行い，求められた信号を表示せよ．

課題3

課題0の信号にHanning Windowをかけた信号を表示せよ．その信号に対して離散フーリエ変換を行い，振幅スペクトルを表示し，課題1の結果と比較せよ．また，離散フーリエ逆変換を行い，求められた信号を表示せよ．

課題4

課題0の信号にBartlett Windowをかけた信号を表示せよ．その信号に対して離散フーリエ変換を行い，振幅スペクトルを表示し，課題1の結果と比較せよ．また，離散フーリエ逆変換を行い，求められた信号を表示せよ．

課題5

課題0の信号にBlackman Windowをかけた信号を表示せよ．その信号に対して離散フーリエ変換を行い，振幅スペクトルを表示し，課題1の結果と比較せよ．また，離散フーリエ逆変換を行い，求められた信号を表示せよ．

課題6

課題0の信号にパラメータ$\beta=0$のKaiser Windowをかけた信号を表示せよ．その信号に対して離散フーリエ変換を行い，振幅スペクトルを表示し，課題1の結果と比較せよ．また，離散フーリエ逆変換を行い，求められた信号を表示せよ．

課題7

課題0の信号にパラメータ$\beta=5$のKaiser Windowをかけた信号を表示せよ．その信号に対して離散フーリエ変換を行い，振幅スペクトルを表示し，課題2の結果と比較せよ．また，離散フーリエ逆変換を行い，求められた信号を表示せよ．

課題8

課題0の信号にパラメータ$\beta=6$のKaiser Windowをかけた信号を表示せよ．その信号に対して離散フーリエ変換を行い，振幅スペクトルを表示し，課題3の結果と比較せよ．また，離散フーリエ逆変換を行い，求められた信号を表示せよ．

課題9

課題0の信号にパラメータ$\beta=8.6$のKaiser Windowをかけた信号を表示せよ．その信号に対して離散フーリエ変換を行い，振幅スペクトルを表示し，課題5の結果と比較せよ．また，離散フーリエ逆変換を行い，求められた信号を表示せよ．